Question

A lens forms an image of an object. The object is 16.0cm from the lens. The image is 12.0cm from the lens on the same side as the object. Part A What is the focal length of the lens? F = cm Part B Is the lens converging or diverging? Is the lens converging or diverging? The lens is converging. The lens is diverging. Part C If the object is 8.50mm tall, how tall is the image? y′ = cm Part D Is it erect or inverted?

Answer 1

A) -48.0 cm

In order to find the focal length of the lens, we can use the lens equation:

`(1)/(f)=(1)/(p)+(1)/(q)`

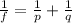
where

f is the focal length

p is the distance of the object from the lens

q is the distance of the image from the lens

In this problem, we have:

p = 16.0 cm

q = -12.0 cm (the negative sign is due to the fact that the image is on the same side as the object, so it is a virtual image, so the sign of q is negative)

Substituting, we find f:

`(1)/(f)=(1)/(16)+(1)/(-12)=-0.020833 cm^(-1) \rightarrow f=-48 cm`

B) Diverging

We have two types of lenses:

- A converging (convex) lens is curved outwards in its center, so that the incoming rays of light parallel to the principal axis are focused into the focus of the lens, on the opposite side

- A diverging (concave) lens is curved inwards in its center, so that the incoming rays of light parallel to the principar axis are deviated away from the principal axis, and they appear to come all from the focal point of the length on the same side of the object

A converging lens is identified by a positive focal length, while the focal length in a diverging lens is negative. Here, f = -48.0 cm, so this is a diverging lens.

C) 6.38 mm

We can answer this part of the problem by using the magnification equation:

`(y')/(y)=-(q)/(p)`

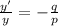
where

y' is the size of the image

y is the size of the object

Here we have:

y = 8.50 mm

p = 16.0 cm

q = -12.0 cm

So we find:

`y' = - (q)/(p)y=-((-12))/(16)(8.50)=6.38 mm`

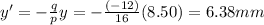
D) Erect

We can determine the orientation of the image by looking at the sign of the size of the image found in part C). In fact:

- if the image is erect, the sign of y' is positive

- if the image is inverted, the sign of y' is negative

In this situation, we see that

y' = 6.38 mm

Which is positive, so the image is erect.