Question

A conductor carries a current that is decreasing exponentially with time. The current is modeled as I = I0e−t/τ, where I0 = 7.75 A is the current at time t = 0.00 s and τ = 0.50 s is the time constant. How much charge flows through the conductor (in C) between t = 0.00 s and t = 2τ? (Enter the magnitude.)

Answer 1

Given:

At t = 0 s and
`\tau` = 0.50s

`I_(o)[\tex] = 7.75 A</p><p>I = [tex]I_(o)e^-{(t)/(\tau)}`

Solution:

Now, to calculate the charge flow in the interval t = 0 to t = 2
`\tau`

We know that, electric current is the rate of flow of electric charge and is given by:

`I = (\Delta Q)/(\Delta T)`

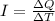
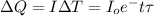`\Delta Q = I\Delta T = I_(o)e^-{\farc{t}{\tau}}` (1)

Integrating the above eqn in the interval t = 0 to t = 2
`\tau`

`\int_(0)^(Q)\Delta Q = \int_(0)^(2\tau)I_(o)e^-{(t)/(\tau)}\Delta T`

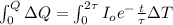
Q =
`[-\tau (I_(o)e^-(t)/(\tau))]_(0)^(2\tau)`

Q =
`I_(o)[-\tau e^(-2) + \tau]`

Q =
`7.75[-0.50 e^(-2) + 0.50]`

Q = 3.35 C

Therefore, Q = 3.35 C of charge flows through the conductor in the given interval.