Answer:
we can say that the cut-off= 476.125 minutes
Explanation:
mean = 445.5 minutes
standard deviation = 22.75 minutes
rate reduction not more than = 9%
The z score corresponding to (100-9)%= 0.91 is 1.35
by standard normal Table
we use

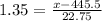
on calculating we get
x= 476.2125 minutes
Therefore, we can say that the cut-off= 476.125 minutes