For this case we have that by definition, the multiplicity of the root of a polynomial is given by the number of times the root is repeated. Example:
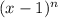
The zero "1" has a multiplicity of "n".
In this case we have the following function:
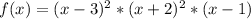
So:
The zero "3" has a multiplicity of "2".
The zero "-2" has a multiplicity of "2".
The zero "1" has a multiplicity of "1".
Answer:
The zero "1" has a multiplicity of "1".
The zero "-2" has a multiplicity of "2".