Question

A certain kind of glass has nblue = 1.64 for blue light and nred = 1.54 for red light. If a beam of white light (containing all colors) in air is incident at an angle of 48°, what is the angle between the red and blue light inside the glass?

Answer 1

The angle between the red and blue light inside the glass is 1.9°.

Step-by-step explanation:

Given that,

Refractive index

For blue = 1.64

For red = 1.54

Incident angle = 48°

We need to calculate the angle between the red and blue light inside the glass

Using Snell's law

`(\sin_(i))/(\sin_(r))=n`

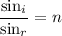
For blue ray,

`\frac{\sin_(i)}{\sin_{r_(b)}}=n_(b)`

`r_(b)=\sin^(-1)(\sin48^(\circ))/(n_(b))`

`r_(b)=\sin^(-1)(\sin48^(\circ))/(1.64)`

`r_(b)=26.95^(\circ)`

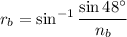
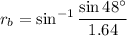
For red ray,

`\frac{\sin_(i)}{\sin_{r_(r)}}=n_(r)`

`r_(r)=\sin^(-1)(\sin48^(\circ))/(n_(r))`

`r_(r)=\sin^(-1)(\sin48^(\circ))/(1.54)`

`r_(r)=28.85^(\circ)`

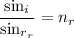
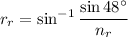
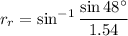
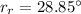
We need to calculate the angle between the red and blue

`r_(rb)=r_(r)-r_(b)`

Put the value into the formula

`r_(rb)=28.85-26.95`

`r_(rb)=1.9^(\circ)`

Hence, The angle between the red and blue light inside the glass is 1.9°.