Question

A 3.50 kg block is pushed along a horizontal floor by a force of magnitude 15.0 N at an angle θ = 30.0° with the horizontal. The coefficient of kinetic friction between the block and the floor is 0.250.

Calculate the magnitudes of (a) the frictional force on the block from the floor and
(b) the block's acceleration.

Answer 1

The frictional force on the block from the floor and the block's acceleration are 10.45 N and 0.73 m/s².

Explanation :

Given that,

Mass of block = 3.50

Angle = 30°

Force = 15.0 N

Coefficient of kinetic friction = 0.250

We need to calculate the frictional force

Using formula of frictional force

`F_(k)=\mu N`

`F_(k)=\mu (F\sin\theta+mg)`

`F_(k)=0.250*(15*\sin30^(\circ)+3.50*9.8)`

`F_(k)=0.250*41.8`

`F_(k)=10.45\ N`

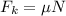
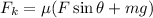
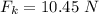
(II). We need to calculate the block's acceleration

Using newton's second law of motion

`F=ma`

`a=(F)/(m)`

`a=(F\cos\theta-F_(k))/(m)`

`a=(15.0\cos30^(\circ)-10.45)/(3.50)`

`a=0.73\ m/s^2`

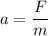
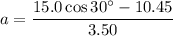
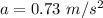
Hence, The frictional force on the block from the floor and the block's acceleration are 10.45 N and 0.73 m/s².