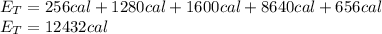Question

16 grams of ice at –32°C is to be changed to steam at 182°C. The entire process requires _____ cal. Round your answer to the nearest whole number. The specific heat of both ice and steam is 0.5 cal/g°C. The specific heat of water is 1.00 cal/gK. The heat of fusion is 80 cal/g and the heat of vaporization is 540 cal/g.

Answer 1

12432 cal.

Step-by-step explanation:

The process to change ice at -32 ºC to steam at 182 ºC can be divided into 5 steps:

1. Heat the ice to 0 ºC, which is the fusion temperature.

2. Melt the ice (obtaining liquid water), which is a process at constant pressure and temperature, so the liquid obtained is also at 0ºC.

3. Heat the liquid water from 0 ºC to 100 ºC, which is the vaporization normal temperature of the water.

4. Vaporization of all the water; this is also a process that occurs at constant pressure and temperature, so the produced steam will be at 100ºC.

5. Heat the steam from 100 ºC to 182 ºC.

Each process has a required energy, and the sum of the energy required for each and all of the steps is the total amount of energy required for the whole process:

`E_T=E_1+E_2+E_3+E_4+E_5`

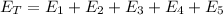
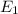`E_1` is a heating process for the ice, so we know that the energy required is proportional to the temperature difference through the specific heat:

`E_1=m*Cp_(sol)*(T_2-T_1)\\E_1=16g*0.5(cal)/(gC)*(0-(-32))=256cal`

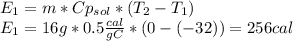
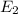`E_2` is a phase change process, so we do not use the specific heat (sensible heat), but the fusion heat (latent heat), so:

`E_(2)=m*dh_(f)={16g*80(cal)/(g)}=1280cal`

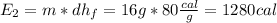
Analogously,

`E_3=m*Cp_(liq)*(T_3-T_2)=16g*1.00(cal)/(gC)*(100-0)C = 1600 cal`

`E_(4)=m*{dh_(vap)}\\\\E_4=16g*540(cal)/(g) =8640cal`

`E_(5)=m*Cp_(vap)*(T_(5)-T_(4))\\E_(5)={16g*0.5(cal)/(gK)*(182-100)K}=656cal`

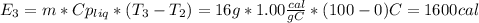
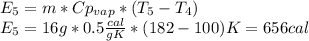
Finally, the total energy required is:

`E_T=256cal+1280cal+1600cal+8640cal+656cal\\E_T=12432cal`