Question

A crate of mass 10.6 kg is pulled up a rough incline with an initial speed of 1.51 m/s. The pulling force is 93.0 N parallel to the incline, which makes an angle of 20.1° with the horizontal. The coefficient of kinetic friction is 0.400, and the crate is pulled 5.08 m.

a) How much work is done by the gravitational force on the crate?
b) Determine the increase in internal energy of the crate-incline system due friction.
c) How much work is done by the 93.0 N force on the crate?
d) What is the change in kinetic energy of the crate? e) What is the speed of the crate after being pulled 5.08 m?

Answer 1

a)
`W_(g) = 181.482\,J`, b)
`W_(f) = 198.370\,J`, c)
`W_(F) = 472.44\,J`, d)
`\Delta K = 92.588\,J`, e)
`v_(f) \approx 4.444\,(m)/(s)`

Step-by-step explanation:

a) The work done by the gravitational force on the crate is:

`W_(g) = (10.6\,kg) \cdot (9.807\,(m)/(s^(2)))\cdot (5.08\,m)\cdot \sin 20.1^(\textdegree)`

`W_(g) = 181.482\,J`

b) The increase in internal energy due to friction is:

`W_(f) = 0.4\cdot (10.6\,kg)\cdot (9.807\,(m)/(s^(2)) )\cdot (5.08\,m)\cdot \cos 20.1^(\textdegree)`

`W_(f) = 198.370\,J`

c) The work done by the external force is:

`W_(F) = (93\,N)\cdot (5.08\,m)`

`W_(F) = 472.44\,J`

d) The change in kinetic energy is obtained from the Principle of Energy Conservation and the Work-Energy Theorem:

`\Delta K = W_(F) - W_(f) - W_(g)`

`\Delta K = 472.44\,J -198.370\,J - 181.482\,J`

`\Delta K = 92.588\,J`

e) The final speed of the crate is:

`\Delta K = (1)/(2)\cdot m \cdot (v_(f)^(2)-v_(o)^(2))`

`v_(f)^(2) = v_(o)^(2) + (2\cdot \Delta K)/(m)`

`v_(f) = \sqrt{v_(o)^(2)+ (2\cdot \Delta K)/(m) }`

`v_(f) = \sqrt{\left(1.51\,(m)/(s)\right)^(2)+(2\cdot (92.588\,J))/(10.6\,kg) }`

`v_(f) \approx 4.444\,(m)/(s)`

Answer 2

a) 181.35 J

b) 198.22 J

c) 465 N

d) 85.42 J

e) 4.28 m/s

Step-by-step explanation:

Given data:

Mass of the crate, m = 10.6 kg

Initial speed of the crate, v = 1.51 m/s

Pulling force, F = 93.0 N

Angle made by the incline, θ = 20.1°

Distance pulled, d = 5.08 m

coefficient of kinetic friction,
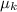`\mu_k` = 0.400

a) The work done by the gravitational force on an inclined plane is given as:

W = m × g × sinθ ×d

where, g is the acceleration due to the gravity

thus,

W₁ = 10.6 × 9.8 × sin 20.1° × 5.08

or

W₁ = 181.35 J

b) Since, work done is the change in energy.Thus, work done by the frictional force is the change in internal energy by the frictional force.

Therefore,

ΔE = (
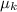`\mu_k`Ncosθ) × d

where, N is the normal reaction

N = mg = 10.6 × 9.8 = 1023.88 N

on substituting the values in the above formula, we get

ΔE = 0.4 × 103.88 × cos20.1° × 5.08

or

ΔE = 198.22 J

c) Work done (W) by the 93 N force will be

W₂ = Force × displacement

or

W₂ = 93 × 5 = 465 N

d) The change in kinetic energy will be the net work done by the system

thus,

Now, considering the work done by the pulling force as positive, thus, work done by the gravitational force and the frictional force will be negative as the both are acting against the pulling force.

Therefore,

ΔK.E = W₂ - W₁ - ΔE

on substituting the values, we get

ΔK.E = 465 - 181.35 - 198.22

or

ΔK.E = 85.42 J

e) we have the change in the kinetic energy as 87.3 J

85.42 = (1/2)mv₂² - (1/2)mv₁²

where,

v₂ is the final velocity bi.e the velocity after being pulled

thus,

85.42 = (1/2) × 10.6 × (v₂² - 1.51²)

or

(v₂² - 1.51²) = 16.11

or

v₂² = 18.397

or

v₂ = √18.397 = 4.28 m/s