Question

An ambulance with a siren emitting a whine at 1790 Hz overtakes and passes a cyclist pedaling a bike at 2.36 m/s. After being passed, the cyclist hears a frequency of 1780 Hz. How fast is the ambulance moving? (Take the speed of sound in air to be 343 m/s.)

Answer 1

The speed of the ambulance is 4.30 m/s

Step-by-step explanation:

Given:

Frequency of the ambulance, f = 1790 Hz

Frequency at the cyclist, f' = 1780 Hz

Speed of the cyclist, v₀ = 2.36 m/s

let the velocity of the ambulance be 'vₓ'

Now,

the Doppler effect is given as:

`f'=f(v\pm v_o)/(v\pm v_x)`

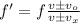
where, v is the speed of sound

since the ambulance is moving towards the cyclist. thus, the sign will be positive

thus,

`v_x=(f)/(f')(v+v_o)-v`

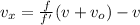
on substituting the values, we get

`v_x=(1790)/(1780)(343+2.36)-343`

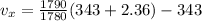
or

vₓ = 4.30 m/s

Hence, the speed of the ambulance is 4.30 m/s