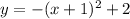Answer:
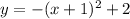 .
.
Explanation:
This is a parabola so it's parent is
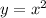 .
.
Let's described what happened to get from the parent to this.
The graph has been reflected so we will have
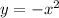 .
.
The graph has been moved left 1 and up 2 so this gives us:
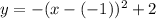 .
.
Simplifying this gives us
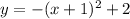 .
.
Let's see if a few points we can identify can help confirm or convince you.
Some points I see that cross nicely are:
(-3,-2)
(-2,1)
(-1,2)
(0,1)
(1,-2)
Let's check them and see.
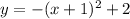 with
with
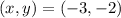 :
:
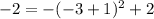

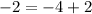
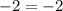 is true so (-3,-2) does satisfy
is true so (-3,-2) does satisfy
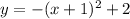 .
.
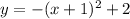 with
with
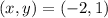 :
:
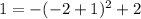
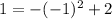

 is true so (-2,1) does satisfy
is true so (-2,1) does satisfy
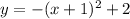 .
.
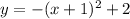 with
with
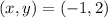 :
:
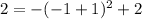
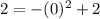
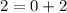
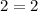 is true so (-1,2) does satisfy
is true so (-1,2) does satisfy
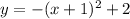 .
.
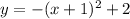 with
with
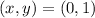 :
:
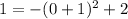
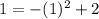

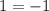 is true so (0,1) does satisfy
is true so (0,1) does satisfy
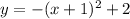 .
.
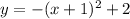 with
with
 :
:

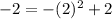
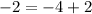
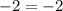 is true so (1,-2) does satisfy
is true so (1,-2) does satisfy
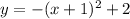 .
.
All the mentioned points satisfied our equation: