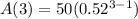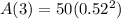Question

5/28

4. You drop a ball from a height of 0.5 meter. Each curved path has 52% of the height of the previous path.
a. Write a rule for the sequence using centimeters. The initial height is given by the term n = 1.
b. What height will the ball be at the top of the third path?
An) - 50 (0.52)* ), 13.52 cm
O A(n) - 0.5 (0.52)*-1, 0.14 cm
A(n) = 50 (52)-1; 135,200 cm
O A(n) = 0.52. (0.5)*-1, 013 cm
305
90%

Answer 1

Part a) The rule of the sequence is
`A(n)=50(0.52^(n-1))`

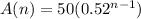
Part b) The height of the ball will be
`13.52\ cm`

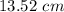
Explanation:

Part a) Write a rule for the sequence using centimeters. The initial height is given by the term n = 1.

we know that

In a Geometric Sequence each term is found by multiplying the previous term by a constant called the common ratio (r)

In this problem we have a geometric sequence

Let

n-----> the number of path

a1 ----> is the initial height

r -----> the common ratio

we have

`a1=0.5\ m=0.5*100=50\ cm`

`r=52\%=52/100=0.52`

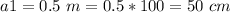
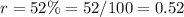
The rule for the sequence is equal to

`A(n)=a1(r^(n-1))`

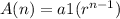
substitute

`A(n)=50(0.52^(n-1))`

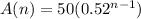
Part b) What height will the ball be at the top of the third path?

For n=3

substitute in the equation

`A(3)=50(0.52^(3-1))`

`A(3)=50(0.52^(2))`

`A(3)=13.52\ cm`