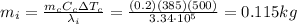Question

A 200.0-g copper cylinder at 500°C is placed on a large block of ice at 0.00°C. Assume that no energy is transferred to the surroundings.

What is the mass of the ice that will melt?

The specific heat of copper is 385 J/kg•°C.

Answer 1

0.115 kg

Step-by-step explanation:

Since no energy is transferred to the surroundings, all the heat from the copper is used to melt the block of ice. So we can write:

`m_c C_c \Delta T_c = m_i \lambda_i`

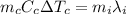
where:

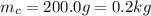`m_c = 200.0 g = 0.2 kg` is the mass of the copper

Cc = 385 J/kg•°C is the specific heat of copper

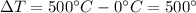`\Delta T = 500^(\circ)C-0^(\circ)C=500^(\circ)` is the change in temperature of the copper (the copper stops to give heat to the ice when they are in thermal equilibrium, so when they have reached the same temperature)

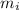`m_i` is the mass of ice

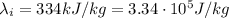`\lambda_i = 334 kJ /kg = 3.34\cdot 10^5 J/kg` is the latent heat of fusion of ice

Solving the equation for the mass of the ice, we find

`m_i = (m_c C_c \Delta T_c)/(\lambda_i)=((0.2)(385)(500))/(3.34\cdot 10^5)=0.115 kg`