a. Note that
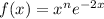 is continuous for all
is continuous for all
 . If
. If
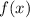 attains a maximum at
attains a maximum at
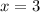 , then
, then
 . Compute the derivative of
. Compute the derivative of
 .
.
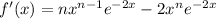
Evaluate this at
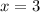 and solve for
and solve for
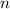 .
.
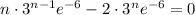
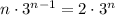
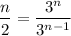
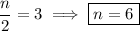
To ensure that a maximum is reached for this value of
 , we need to check the sign of the second derivative at this critical point.
, we need to check the sign of the second derivative at this critical point.
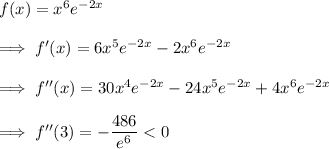
The second derivative at
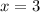 is negative, which indicate the function is concave downward, which in turn means that
is negative, which indicate the function is concave downward, which in turn means that
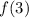 is indeed a (local) maximum.
is indeed a (local) maximum.
b. When
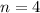 , we have derivatives
, we have derivatives
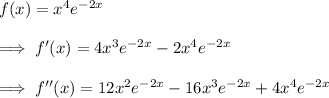
Inflection points can occur where the second derivative vanishes.
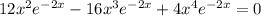
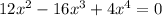
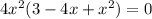
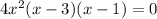
Then we have three possible inflection points when
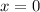 ,
,
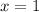 , or
, or
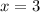 .
.
To decide which are actually inflection points, check the sign of
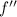 in each of the intervals
in each of the intervals
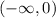 ,
,
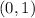 ,
,
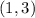 , and
, and
 . It's enough to check the sign of any test value of
. It's enough to check the sign of any test value of
 from each interval.
from each interval.

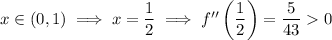
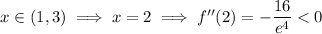
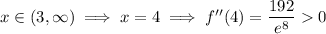
The sign of
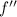 changes to either side of
changes to either side of
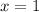 and
and
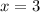 , but not
, but not
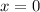 . This means only
. This means only
 and
and
 are inflection points.
are inflection points.