Answer:
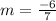
Explanation:
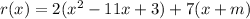
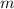 is constant.
is constant.
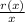 has no remainder. This would mean
has no remainder. This would mean
 is a factor of
is a factor of
 .
.
By factor theorem if x-c is a factor of r then r(c)=0.
We have that x or x-0 is a factor of r:
By factor theorem if x-0 is a factor of r then r(0)=0.
So let's plug in 0 for x:
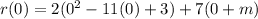
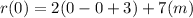
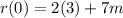
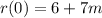
Now again we have r(0)=0 since x is a factor of r.
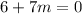
Subtract 6 on both sides:
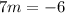
Divide both sides by 7:
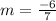
----------------------------------------------------------------------------------
Another way.
So since
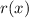 is divisible by
is divisible by
 that means when we divide
that means when we divide
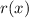 by
by
 we will have no fractions.
we will have no fractions.
So let's do that:
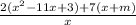
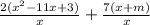
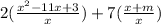
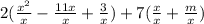
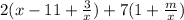
I'm going to get my fractions together.
Distribute the 2 to the terms in the ( ) next to it. Distribute 7 to the terms in the ( ) next to it:
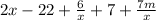
Reorder using commutative property of addition:
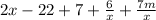
Combine like terms ( the fractions too since the denominators are the same):
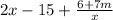
Again we wanted no fraction.
A fraction is 0 when the numerator is 0.
If we find when 6+7m is 0, then we have found the value of m for which x divides r(x).
6+7m=0
Subtract 6 on both sides:
7m=-6
Divide both sides by 7:
m=-6/7.