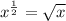Question

What is 1/x∧-3/6 and how do you get to that answer?

Answer 1

`x^(1)/(2)`

or

`√(x)`

Explanation:

`(1)/(x^(-3)/(6))`

I'm going to reduce -3/6 to -1/2 by dividing top and bottom of -3/6 by 3.

`(1)/(x^(-1)/(2))`

Now I'm going to get rid of the negative exponent by moving x to the top; so -1/2 will change to 1/2 instead when doing this:

`1x^(1)/(2)`

`x^(1)/(2)`

`√(x)`

Please let know if I read the problem right:

`(1)/(x^(-3)/(6))`

Answer 2

The answer is
`√(x)`

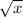
Explanation:

Step 1: Deal with the negative exponent applying this rule:

`x^(-b) = (1)/(x^(b))`

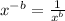
In this case

`b=- (3)/(6)`

Putting all together:

`\frac{1}{x^{-(3)/(6)}} =x^{-(-(3)/(6)) } =x^{(3)/(6)}`

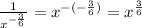
Step 2: Reduce the fractional exponent

The fractional exponent
`(3)/(6)` can be reduced dividing the numerator and denominator of the fraction by the least common multiple.

In order to find it, we have

`3=(3)*(1)\\6=(3)*(2)\\`

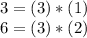
Therefore, the least common multiple is 3

Reducing the fraction:

`(3)/(6)=(3/3)/(6/3)=(1)/(2)`

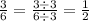
Therefore:

`x^{(3)/(6)}=x^{(1)/(2)}`

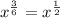
Step 3: Deal with the fractional exponent

A fractional exponent can be expressed as a root, following this rule:

`x^{ (a)/(b)} = \sqrt[b]{x^(a)}`

In this case:

`a=1\\b=2`

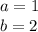
As the index of the root is 2, this is a square root, therefore:

`x^{(1)/(2)} = √(x)`