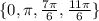Question

PLEASE HURRY I NEED HELP SOS!!!!!!!! (10 POINTS)

solve sinø+1=cos2ø on the interval 0≤ø<2π

Answer 1

`\{0,\pi , (7\pi)/(6),(11\pi)/(6)\}`

Explanation:

We are going to have to use a double angle identity.

`\cos(2\theta)=\cos^2(\theta)-\sin^2(\theta)`

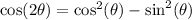
I'm going to write this in terms of sine since the left hand side of the equation is also in terms of sine.

So applying the Pythagorean Identity
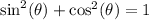`\sin^2(\theta)+\cos^2(\theta)=1` to the identity above gives you:

`\cos(2\theta)=(1-\sin^2(\theta))-\sin^2(\theta)`

`\cos(2\theta)=1-2\sin^2(\theta)`

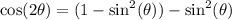
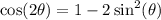
So the equation you have becomes:

`\sin(\theta)+1=1-2\sin^2(\theta)`

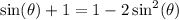
Get one side to be 0.

I'm going to move everything on right side to left side.

When you move a term over from one side to another, you just need to change the sign in front it. so if is plus 1 on the right it is minus 1 on the left.

If it is minus
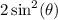`2\sin^2(\theta)` then it is plus
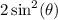`2\sin^2(\theta)` on the other side.

`2\sin^2(\theta)+\sin(\theta)+1-1=0`

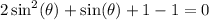
Combine the like terms (1-1):

`2\sin^2(\theta)+\sin(\theta)+0=0`

`2\sin^2(\theta)+\sin(\theta)=0`

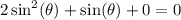
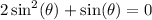
Factor out the common factor on the left which is sin( )[/tex]

`\sin(\theta)[2\sin(\theta)+1]=0`

If you have a product is 0 then one of the factors must be zero (both could be 0 also).

`\sin(\theta)=0` or
`2\sin(\theta)+1=0`

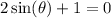
I'm going to solve the first equation first.

`\sin(\theta)=0` when the y-coordinate on the unit circle is 0.

This happens at
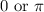`0 \text{ or } \pi` is the given interval you provided.

Let's solve the other equation:

`2\sin(\theta)+1=0`

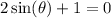
Subtract 1 on both sides:

`2\sin(\theta)=-1`

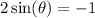
Divide both sides by 2:

`\sin(\theta)=(-1)/(2)`

So you are looking for when the y-coordinate is -1/2 on the unit circle.

This happens at
`(7\pi)/(6) \text{ or } (11\pi)/(6)`

So the solution set is:

`\{0,\pi , (7\pi)/(6),(11\pi)/(6)\}`

Answer 2

`\theta \in \{0, \pi, (11\pi)/(6)\}`

Explanation:

`\sin\theta + 1 = \cos(2\theta)\\\sin\theta + 1 = \cos^2\theta - \sin^2\theta\\\sin\theta + \sin^2\theta + \cos^2\theta = cos^2\theta -\sin\theta^2\\2\sin^2\theta +\sin\theta = 0\\\sin\theta[2\sin\theta + 1] = 0\\\sin\theta = 0 || 2\sin\theta + 1 = 0\\\theta \in \{0, \pi, (11\pi)/(6)\}`