Answer:
516
Explanation:
Let's start with the value first to see if we can use
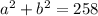 to help find it's value:
to help find it's value:
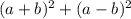
I'm going to use the formula
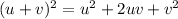 to expand both:
to expand both:

Combining like terms:

Factoring the 2 out:

Plug in 258 for the
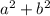 :
:
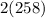
Perform the multiplication:
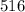
-----------------------------------------------
Another way:
Find values for
 and
and
 that satisfy:
that satisfy:
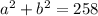
The easiest solution you might see is
 . This works because the square of
. This works because the square of
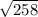 is 258.
is 258.
So now you just plug:
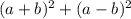 with
with
 being
being
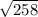 and
and
 being 0 into your calculator or if you are good at simplifying things without you can do that with this problem:
being 0 into your calculator or if you are good at simplifying things without you can do that with this problem:
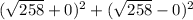
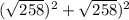

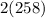
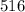
This would have worked for any pair
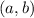 satisfying
satisfying
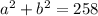 .
.
I wanted to show this last strategy just in case you haven't been exposed to expanding squared binomials with foil or the formula I mentioned earlier.