Answer:
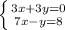
Explanation:
An equivalent system refer to other system that has the same values for the variables, or it's satisfied by the same values. First, we calculate what are the values for x and y, in the given system.
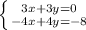
Extracting common factors:
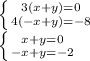
Now, summing both equations we have:
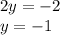
Replacing this value in a equation we have:
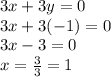
Now, we have to find the other system that it's satisfied by
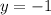 and
and
 .
.

As you can see, the first system is equivalent because it has the same solution as the given system of equations.
Therefore, the correct answer is the first one.