For this case we have that by definition, a direct variation is represented as:

While an inverse variation is represented as:
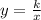
If we have that Q varies inversely as the square of p means that:
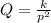
Substituting the values and clearing the proportionality constant we have:
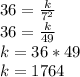
Now we must find the value of Q when
 :
:
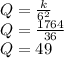
Answer:
Option C