Question

What is the value of X ? Explain ( chords and arcs )

Answer 1

x ≈ 9.4

Explanation:

The segment from the centre is a perpendicular bisector of the chord.

Using Pythagoras' identity in the right triangle formed with hypotenuse 13 and legs 9 and x

The square on the hypotenuse is equal to the sum of the squares on the other 2 sides, that is

x² + 9² = 13²

x² + 81 = 169 ( subtract 81 from both sides )

x² = 88 ( take the square root of both sides )

x =
`√(88)` = 2
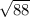`√(22)` ≈ 9.4 ( to 1 dec. place )

Answer 2

Basic points to remember

1) perpendicular drawn from centre always bisects chord

2) diameter is double of radius

Now get revert back to Question

18= chord length

So, chord/2 = 18/2 = 9

26 = diameter

26/2 = 13= radius

Now As it forms right angled triangle

Hence

x= √( 13^2 - 9^2)

= √169-81

= √88

= 2√22