Question

Please answer the attached question by selecting of the the given answers.

Answer 1

`\frac{2 {x}^(2) - 4x - 6}{x + 2} . \frac{ {x}^(2) - 4}{2 {x}^(2) + 2x } \\ \\ = \frac{2 {x}^(2) + 2x - 6x - 6}{x + 2} . \frac{ {x}^(2) - 4}{2x(x + 1) } \\ \\ = (2x(x + 1) - 6(x + 1))/(x + 2) . \frac{ {x}^(2) - 4}{2x(x +1)} \\ \\ ((2x - 6)(x + 1))/(x + 2) . \frac{ {x}^(2) - 4 }{2x(x + 1)} \\ \\ = (2x - 6)/(x + 2) . ((x - 2)(x + 2))/(2x) \\ \\ = (2x - 6). (x - 2)/(2x) \\ \\ = (2(x - 3))/(2x) .(x - 2) \\ \\ = (x - 3)/(x) .(x - 2)`

Option A)

Answer 2

For this case we must simplify the following expression:

`(2x^2-4x-6)/(x+2)*(x^2-4)/(2x^2+2x)`

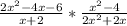
So, by rewriting we have:

`2x^2-4x-6=2(x^2-2x-3)`

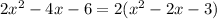
We factor the parenthesis trinomial by looking for two numbers that, when multiplied, are obtained -3 and when added together, -2 is obtained. These numbers are -3 and 1, so:

`2(x^2-2x-3)=2(x-3)(x+1)`

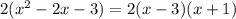
On the other hand we have to:

`x ^ 2-4 = (x-2) (x + 2)`

Last we have:

`2x ^ 2 + 2x = 2x (x + 1)`

Thus, rewriting the expression:

`\frac {2 (x-3) (x + 1)} {x + 2} * \frac {(x-2) (x + 2)} {2x (x + 1)} =`

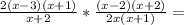
Simplifying:

`\frac {(x-3) (x-2)} {x}`

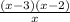
Answer:

Option A