Question

Explain/show why the table below represents a proportional relationship

Answer 1

The table not represent a proportional relationship

Explanation:

we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
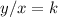`y/x=k` or
`y=kx`

In a proportional relationship the constant of proportionality k is equal to the slope m of the line and the line passes through the origin

we have

For x=3, y=17

Find the value of k

`k=y/x` ----->
`k=17/3=5.67`

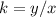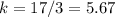
For x=5, y=27

Find the value of k

`k=y/x` ----->
`k=27/5=5.4`

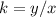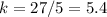
For x=8, y=42

Find the value of k

`k=y/x` ----->
`k=42/8=5.25`

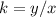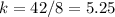
For x=9, y=47

Find the value of k

`k=y/x` ----->
`k=47/9=5.22`

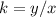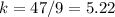
The values of k are different

therefore

The table not represent a proportional relationship

Find the slope of the line

(3,17) and (9,47)

m=(47-17)/(9-3)=30/6=5

Find the equation of the line with m=5 and point (3,17)

y-y1=m(x-x1)

substitute

y-17=5(x-3)

y=5x-15+17

y=5x+2

This is the linear equation that represent the points in the table, but this equation not represent a proportional relationship (The line not passes through the origin)