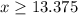Question

Write an inequality for x that

would give this rectangle an
area of at least 246 it?.
8m
(2x + 4)m

Answer 1

14

Explanation:

Answer 2

Question 1:

For this case we must solve the following expression:

`\frac {k} {3} + 4-2k = -9k`

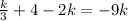
Adding 9k to both sides of the equation we have:

`\frac {k} {3} + 4-2k + 9k = -9k + 9k\\\frac {k} {3} + 4 + 7k = 0`

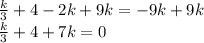
Subtracting 4 from both sides of the equation:

`\frac {k} {3} + 4-4 + 7k = -4\\\frac {k} {3} + 7k = -4\\\frac {k + 21k} {3} = - 4\\\frac {22k} {3} = - 4\\`

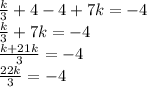
Multiplying by 3 on both sides:

`22k = -12`

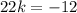
Dividing between 22 on both sides:

`k = \frac {-12} {22}\\k = - \frac {6} {11}`

Answer:

`k = - \frac {6} {11}`

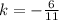
Question 2:

For this case we have that by definition, the area of the rectangle is given by:

`A = a * b`

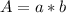
Where a and b are the sides of the rectangle.

If the area is at least
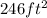`246ft ^ 2` we have:

`A \geq246`

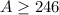
That is to say:

`8 (2x + 4) \geq246\\16x + 32 \geq246\\16x \geq246-32\\16x \geq214\\x \geq \frac {214} {16}\\x \geq13.375`

Answer:

`x \geq13.375`