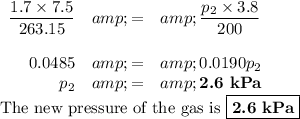Answer:
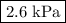
Step-by-step explanation:
To solve this problem, we can use the Combined Gas Laws:
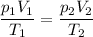
Data:
p₁ = 1.7 kPa; V₁ = 7.5 m³; T₁ = -10 °C
p₂ = ?; V₂ = 3.8 m³; T₂ = 200 K
Calculations:
(a) Convert temperature to kelvins
T₁ = (-10 + 273.15) K = 263.15 K
(b) Calculate the pressure