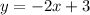Question

whats the equation for the perpendicular bisector of the line segment whose endpoints are (-5,3) and (3,7)?

Answer 1

The equation of perpendicular bisector of the line segment passing through (-5,3) and (3,7) is:
`y = -2x+3`

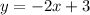
Explanation:

Given points are:

(-5,3) and (3,7)

The perpendicular bisector of line segment formed by given points will pass through the mid-point of the line segment.

First of all we have to find the slope and mid-point of given line

Here

(x1,y1) = (-5,3)

(x2,y2) = (3,7)

The slope will be:

`m = (y_2-y_1)/(x_2-x_1)\\m = (7-3)/(3+5)\\m = (4)/(8)\\m = (1)/(2)`

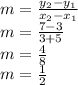
The mid-point will be:

`(x,y) = ((x_1+x_2)/(2) , (y_1+y_2)/(2))\\ = ((-5+3)/(2),(3+7)/(2))\\= ((-2)/(2),(10)/(2))\\=(-1,5)`

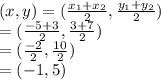
Let m1 be the slope of the perpendicular bisector

Then using, "Product of slopes of perpendicular lines is -1"

`m.m_1 = -1\\(1)/(2).m_1 = -1\\m_1 = -1*2\\m_1 = -2`

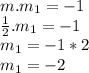
We have to find the equation of a line with slope -2 and passing through (-1,5)

The slope-intercept form is given by:

`y = mx+b\\y = -2x+b`

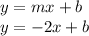
Putting the point (-1,5) in the equation

`5 = -2(-1)+b\\5 = 2+b\\b = 5-2\\b = 3`

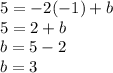
The final equation is:

`y = -2x+3`

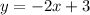
Hence,

The equation of perpendicular bisector of the line segment passing through (-5,3) and (3,7) is:
`y = -2x+3`