Question

Determine if the equation below is a function with independent variable x. If so, find the domain. If not, find a value of x to which there corresponds more than one value of y.

x^{2} +y^{2} =25

Answer 1

No because it contains points (3,4) and (3,-4). You cannot have a x assigned to more than one y-value if you want it to be a function.

Explanation:

A function has one output per input.

If we are trying to determine if the given is a function of x, then x is the input.

However I can get two outputs from plugging in x=3.

`3^2+y^2=25`

`9+y^2=25`

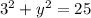
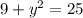
Subtract 9 on both sides:

`y^2=25-9`

`y^2=16`

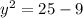
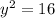
Take the square root of both sides:

`y=\pm √(16)`

`y=\pm 4`.

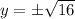
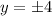So input x=3 yields y=4 and y=-4.

Since this input has more than one output then the given is not a function of x.

----Also!

If you graph the equation, it is a circle with radius 5 and center (0,0). So I could I plug in any number for x between -5 and 5 excluding -5 and 5 which would yield only one output each. Since plugging in either one gives:

`(\pm 5)^2+y^2=25`

`25+y^2=25`

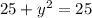
Subtract 25 on both sides:

`y^2=25-25`

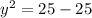
Simplify:

`y^2=0`

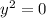
There is only one value y such that when you square it gives you 0. That is 0.

x=5 only gives y=0 and x=-5 only gives y=0.

There is no circle, unless it is a circle with radius 0 which means it really wouldn't be a circle, that is a function.