Question

PLEASE HELP 25PTS!! Select the correct answer from each drop-down menu.

The given function models the number of cars that are put through a quality control test each hour at a car production factory. Some cars are kept overnight at the quality control facility, while some cars arrive at different times of the day.


c(t)= -t^2+8t+20


For how many hours does the quality control facility operate each day?


The best form of the equation for finding the required information is (factored form, standard form, vertex form) . The quality control facility operates for (5,10,8,12) hours each day.

Answer 1

The quality control facility operates for 10 hours each day.

Explanation:

The given function models the number of cars that are put through a quality control test each hour at a car production factory.

The given function is

`c(t)= -t^2+8t+20`

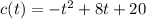
We need to find the number of hours does the quality control facility operate each day.

Rewrite the given function it factored form.

`c(t)= -t^2+(10t-2t)+20`

`c(t)= (-t^2+10t)+(-2t+20)`

Taking out the common factors from each parenthesis.

`c(t)= -t(t-10)-2(t-10)`

`c(t)= (t-10)(-t-2)`

`c(t)=-(t-10)(t+2)`

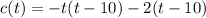
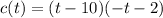
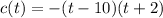
The factored form of given function is c(t)=-(t-10)(t+2).

Equate the function equal to 0 to find the x-intercept.

`0=-(t-10)(t+2)`

`t-10=0\Rightarrow t=10`

`t+2=0\Rightarrow t=-2`

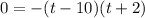
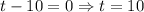
Number of hours cannot be negative. So from t=0 to t=10 quality control facility operate the cars.

Therefore the quality control facility operates for 10 hours each day.