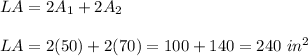Question

50 Points thanks for the help :)

QUESTION 3

Calculate the lateral area of a cube with side measurement of 4.1 ft.

64 cu. ft.

16 sq. ft.

67.24 sq. ft.

66 cu. ft.
2 points

QUESTION 4

Find the surface area of a cylinder with a diameter of 62 cm. and a height of 85 cm.

22582.88 sq. cm.

23045 sq. cm.

22582.88 cu. ft.

19565.34 sq. cm.
2 points


QUESTION 6

Find the surface area of a pyramid with a square base with sides measuring 5 cm. and whose slant height is 9 cm.

115 sq. cm.

110 sq. cm.

22.5 sq. cm.

90 sq. cm.
2 points


QUESTION 10

Find the lateral area of a rectangular prism with base measuring 5 in. by 7 in. and height of 10 in.

350 cu. in.

350 sq. in.

240 sq. in.

289 sq. in.

Answer 1

Q3. 67.24 sq. ft.

Q4. 22582.88 sq. cm.

Q6. 115 sq. cm.

Q10. 240 sq. in.

Explanation:

Q3.

The formula of a lateral area of a cube with side s:

`LA=4s^2`

We have s = 4.1 ft.

Substitute:

`LA=4(4.1^2)=4(16.81)=67.24\ ft^2`

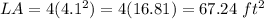
Q4.

The formula of a surface area if a cylinder:

`SA=2\pi r^2+2\pi rH`

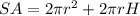
r - radius

H - height

We have 2r = 62 cm → r = 31 cm, H = 85 cm.

Substitute:

`SA=2\pi(31^2)+2\pi(31)(85)=2\pi(961)+5270\pi=1922\pi+5270\pi=7192\pi\ cm^2`

`\pi\approx3.14\to SA\approx(7192)(3.14)=22582.88\ cm^2`

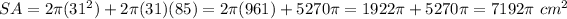
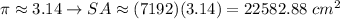
Q6.

The surface area of a square piramid is

base - square

lateral sides - four triangles

The formula of an area of a square with sides s:

`A=s^2`

The formula of an area of a triangle with base b and height h:

`A=(bh)/(2)`

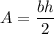
We have s = 5 cm, b = s = 5 cm, h = 9 cm.

Substitute:

`A_(\square)=5^2=25\ cm^2\\\\A_(\triangle)=((5)(9))/(2)=(45)/(2)=22.5\ cm^2`

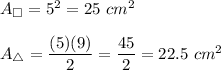
The surface area:

`SA=A_(\square)+4A_(\triangle)\\\\SA=25+4(22.5)=25+90=115\ cm^2`

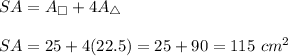
Q10.

The lateral sides are two pairs of rectangles.

The formula of an area of a rectangle:

`A=l\cdot w`

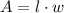
l - length

w - width

We have the rectangles:

5 in × 10 in and 7 in × 10 in

Substitute:

`A_1=(5)(10)=50\ in^2\\\\A_2=(7)(10)=70\ in^2`

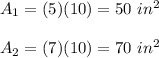
The lateral area:

`LA=2A_1+2A_2\\\\LA=2(50)+2(70)=100+140=240\ in^2`