Question

Compare the functions shown below:

h(x)
f(x) = 2 sin (3x + Tt) - 2 g(x) = (x - 3)2 - 1
Which function has the smallest minimum y-value?

Answer 1

h had the lowest because -6 is less than both -4 and -1.

Explanation:

The range of
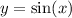`y=\sin(x)` is
`-1\le y\le 1`.

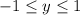The range of
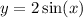`y=2\sin(x)` is
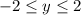`-2\le y \le 2` since the amplitude has been changed from 1 or 2. (It has been vertically stretched.)

The range of
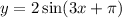`y=2\sin(3x+\pi)` still had range
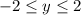`-2\le y \le 2` because changing inside only effects the period and phase shift.

The range of
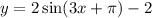`y=2\sin(3x+\pi)-2` would have range
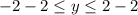`-2-2 \le y \le 2-2` and after simplifying this you get the range is
`-4\le y\le 0`.

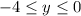The smallest value obtained by function f is -4.

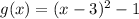`g(x)=(x-3)^2-1` is a parabola in vertex form. The vertex is where the maximum or minimum of a parabola will occur. It has a minimum since the coefficient of
`x^2` is positive.

Comparing to
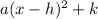`a(x-h)^2+k` where the vertex is (h,k) we should see that the vertex of g is at (3,-1). So the lowest y obtain by this parabola is -1.

So g lowest y is -1.

h is a list of points. All you have to do is look through the second column to see which y is the lowest.

The lowest y there is -6 because -6 is less than all the other y's they have listed.

h has the lowest.

g has the highest.

Answer 2

The function with the smallest minimum y-value is h(x).

Explanation:

f(x) = 2 sin (3x + π) - 2

The minimum value of the sine function is -1 so f(x) has a minimum value of

2 *-1 -2 = -4.

g(x) = (x - 3)^2 - 1

The minimum values of (x - 3)^2 is 0 so minimum for g(x) = -1.

From the table the minimum value for h(x) is -6.