Question

3^2x-6(3^x)-27=0

Hi, I was prepping for my finals when i came along this question, i could not solve it, so could someone please help me and explain the answer. Thank you.​

Answer 1

2

Explanation:

This is a quadratic in terms of
`3^x`.

`(3^x)^2-6(3^x)-27=0`

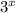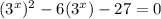
I'm going to substitute
`u=3^x`:

`u^2-6u-27=0`

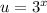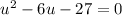
This is actually factorable since all you have to do is find two numbers that multiply to be -27 and add to be -6.

These numbers are -9 and 3 since (-9)(3)=-27 while -9+3=-6.

`(u-9)(u+3)=0`

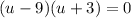
This implies that either u-9=0 or u+3=0.

u-9=0 when u=9. (I added 9 on both sides here.)

u+3=0 when u=-3. (I subtracted 3 on both sides here.)

Recall the substitution:

`u=3^x`

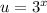
So replacing our solutions that are in terms of u to in terms of x:

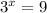`3^x=9` or
`3^x=-3`

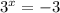
The second equation has no real solution.
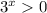`3^x>0` for all x.

So there is no way you find an x such that
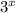`3^x` would be negative.

We only need to solve:

`3^x=9`

`3^x=3^2`

`x=2`

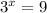
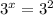
Check:

Replace x with 2 in given problem:

`3^{2\cdot 2)-6(3^2)-27=0`

`3^4-6(9)-27=0`

`81-54-27=0`

`27-27=0`

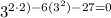
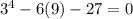
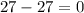
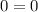`0=0` which is a true equation so x=2 checks out.