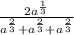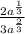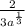Question

Please solve this question no C...​

Answer 1

`\frac{2}{3a^{(1)/(3)}}`

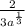
Explanation:

`\lim_(x \rightarrow a)(f(x)-f(a))/(x-a)=f'(a)`.

`f(x)=x^(2)/(3)`

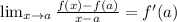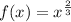
Using power rule we get that
`f'(x)=(2)/(3)x^{-(1)/(3)}`

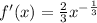
Evaluating this at
`x=a` gives us:
`f'(a)=(2)/(3)a^{-(1)/(3)}`.

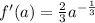We could write without negative exponent giving us:

`f'(a)=\frac{2}{3a^{(1)/(3)}}`.

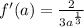We could also go about it an algebraic way.

Notice the numerator is a difference of squares and can be factored as
`(x^(1)/(3)-a^(1)/(3))(x^(1)/(3)+a^(1)/(3))`.

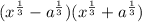We need a factor in the numerator to be
`x-a` so we can get rid of the
`x-a` on bottom and then substitute
`a` for
`x`.

Recall the difference of cubes formula:

`p^3-q^3=(p-q)(p^2+pq+q^2)`

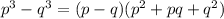
We are going to use this on the denominator:

`(x^(1)/(3))^3-(a^(1)/(3))^3`

`(x^(1)/(3)-a^(1)/(3))(x^(2)/(3)+x^(1)/(3)a^(1)/(3)+a^(2)/(3))`

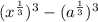
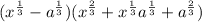
So that first factor there will actually cancel with a factor I mentioned for the numerator earlier.

Let's see it all together:

`\lim_(x \rightarrow a)((x^(1)/(3)-a^(1)/(3))(x^(1)/(3)+a^(1)/(3)))/((x^(1)/(3)-a^(1)/(3))(x^(2)/(3)+x^(1)/(3)a^(1)/(3)+a^(2)/(3)))`

After the cancellation we have:

`\lim_(x \rightarrow a)((x^(1)/(3)+a^(1)/(3)))/((x^(2)/(3)+x^(1)/(3)a^(1)/(3)+a^(2)/(3)))`

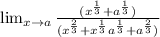
Now we are ready to replace
`x` with
`a`.

`(a^(1)/(3)+a^(1)/(3))/(a^(2)/(3)+a^(1)/(3)a^(1)/(3)+a^(2)/(3))`

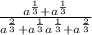
We have some like terms to combine:

`\frac{2a^{(1)/(3)}}{a^(2)/(3)+a^{(2)/(3)}+a^(2)/(3)}`

`(2a^(1)/(3))/(3a^(2)/(3))`

`\frac{2}{3a^{(2)/(3)-(1)/(3)}}`

`\frac{2}{3a^{(1)/(3)}}`