Question

Converges and Diverges part 3:
​

Answer 1

Converges to 2100

Explanation:

This is comparable to:

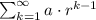`\sum_(k=1)^\infty a \cdot r^(k-1)` where:

r is the common ratio and
`a` is the first term.

The series converges to:

`\text{First term}\cdot \frac{1}{1-\text{common ratio}}`

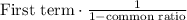
if the ratio's absolute value is less than 1.

This is a geometric series.

The common ration is .8 .

The first term in the series is 420.

Since the |.8|<1, then the series converges to a sum.

The formula for finding the sum is:

`\text{First term}\cdot \frac{1}{1-\text{common ratio}}`

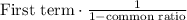
Plugging in our numbers:

`420\cdot (1)/(1-.8)`

`420\cdot (1)/(.2)`

`420\cdot 5`

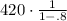
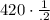
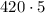
2100