Answer:
It is identity.
It is true for any x in the domain of the equation.
Explanation:
Recall the Pythagorean Identity:
 .
.
Divide both sides be
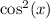 :
:
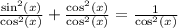
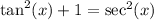 .
.
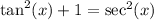 is also known as a Pythagorean Identity as well.
is also known as a Pythagorean Identity as well.
I'm going to apply this last identity I wrote to your equation on the left hand side.
Replacing
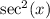 with
with
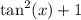 :
:
![-\tan^2(x)+[\tan^2(x)+1]](https://img.qammunity.org/2020/formulas/mathematics/college/hkfiicta7ra0tm4wppzq9wa6at85rxvx3b.png)
Distribute:
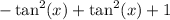
Combine like terms:
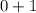

This is what we also have on the right hand side so we have confirmed your given equation is an identity.