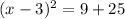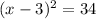Answer:
D.
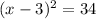
Explanation:
Its looks like they have complete the square for the given equation.
So let's do that.
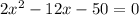
I see all of my terms are even so I can easily divide each of them by 2.
I'm going to divide both sides by 2:
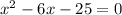
The first step in completing the square is to make sure the coefficient of
 is 1 so we can use this easy formula:
is 1 so we can use this easy formula:
 .
.
So I see in place of k I have -6.
I'm going to add
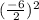 on both sides.
on both sides.
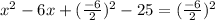
See these first three terms here can be written using the mentioned formula:
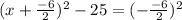
Let's simplify a bit:
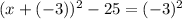
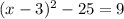
Add 25 on both sides: