Answer:
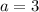 and
and
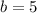 .
.
Explanation:
So I believe the problem is this:
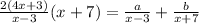
where we are asked to find values for
 and
and
 such that the equation holds for any
such that the equation holds for any
 in the equation's domain.
in the equation's domain.
So I'm actually going to get rid of any domain restrictions by multiplying both sides by (x-3)(x+7).
In other words this will clear the fractions.
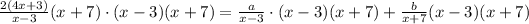
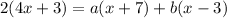
As you can see there was some cancellation.
I'm going to plug in -7 for x because x+7 becomes 0 then.
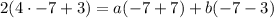
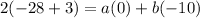
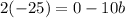
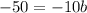
Divide both sides by -10:
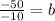
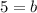
Now we have:
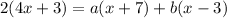 with
with
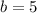
I notice that x-3 is 0 when x=3. So I'm going to replace x with 3.
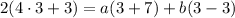
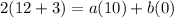
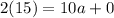

Divide both sides by 10:
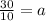
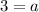
So
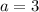 and
and
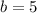 .
.