Question

The seller of a loaded die claims that it will favor the outcome 6. We don’t believe that claim, and roll the die 200 times to test an appropriate hypothesis. Our P-value turns out to be 0.03. Which conclusion is appropriate? Explain. There’s a 3% chance that the die is fair. There’s a 97% chance that the die is fair. There’s a 3% chance that a loaded die could randomly produce the results we observed, so it’s reasonable to conclude that the die is fair. There’s a 3% chance that a fair die could randomly produce the results we observed, so it’s reasonable to conclude that the die is loaded.

Answer 1

Option 3 - There 's a 3% chance that a loaded die could randomly produce the results we observed, so it's reasonable to conclude that the die is fair.

Explanation:

Given : The seller of a loaded die claims that it will favor the outcome 6.

We don’t believe that claim, and roll the die 200 times to test an appropriate hypothesis.

To find : Which conclusion is appropriate? Explain.

Solution :

Our P-value turns out to be 0.03.

i.e.
`P=0.03=3\%`

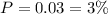
As die favors 6 (when no favoring, we have 1 chance in 6 to roll a 6).

The claim is either the null hypothesis or the alternative hypothesis.

i.e. Null hypothesis
`H_o: p=(1)/(6)`

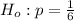
Alternative hypothesis
`H_a: p>(1)/(6)`

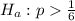
The P-value is the probability of obtaining the value of the test statistic, when the hypothesis is true.

In this case,

There is a 3% chance of obtaining a sample proportion higher than
`(1)/(6)`, when the die is not loaded or fair.

So, option 3 is correct.

There 's a 3% chance that a loaded die could randomly produce the results we observed, so it's reasonable to conclude that the die is fair.