Question

Three electromagnetic waves arrive at a point from the same direction. They are polarized parallel to an x axis, and their electric fields at the point are E1 = A sin(ωt) for wave 1, E2 = B sin(ωt + φ2) for wave 2, and E3 = C sin(ωt + φ3) for wave 3. Here t is time. The constants are A = 3.0 µV/m, B = 4.0 µV/m, C = 5.0 µV/m, ω = 7.0 × 106 rad/s, φ2 = π/4, and φ3 = π/2. What is the amplitude (in µV/m) of the electric field that results from the interference of the three waves?

Answer 1

E₁ = 9.759
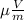`{\mu(V)/(m)}`sin(7.0 × 10⁶ t)

Step-by-step explanation:

Given:

E₁ = 3sin(7.0 × 10⁶ t)

E₂ = 4sin(7.0 × 10⁶ t + 45°)

E₃ = 5sin(7.0 × 10⁶ t + 90°)

Now,

the net vertical component of Electric field E is

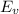`E_v`= 3sin(0°) + 4sin(0° + 45°) + 5sin(0° + 90°)

or

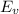`E_v` = 7.828
`{\mu(V)/(m)}`

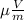
Now,

the net horizontal component of Electric field E is

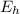`E_h` = 3cos(0°) + 4cos(0° + 45°) + 5cos(0° + 90°)

or

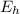`E_h` = 5.828
`{\mu(V)/(m)}`

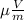
Therefore, the resultant Electric field is

`E_(R) =√(E_v^2+E_h^2)`

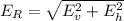
or

`E_(R) =√(7.828^2+5.828^2)`

or

`E_(R) =9.759\ {\mu(V)/(m)}`

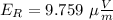
Now, the phase angle is given as:

`\phi=\tan^(-1)(0)/(9.759) =`

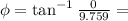
hence,

E₁ = 9.759
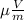`{\mu(V)/(m)}`sin(7.0 × 10⁶ t)