Question

If a football player passes a football from 4 feet off the ground with an initial velocity of 36 feet per second, how long will it take the football to hit the ground? Use the equation h = −16t^2 + 6t + 4. Round your answer to the nearest hundredth.

A) 0.72
B) 0.65
C) 0.35
D) 0.27

Answer 1

Option A is correct

Explanation:

The given equation is

h = -16t^2+6t+4

When the ball will hit the ground, height h = 0

Putting value of h = 0

0 = -16t^2+6t+4

Now solving to find the value of t

=> -16t^2+6t+4 = 0

Multiply with -1

16t^2-6t-4=0

Using quadratic formula to find value of t

`x=(-b\pm√(b^2-4ac))/(2a)`

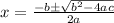
a= 16, b= -6 and c= -4

Putting values,

`t=(-(-6)\pm√((-6)^2-4(16)(-4)))/(2(16))\\t=(6\pm√(36+256))/(32)\\t=(6\pm√(292))/(32)\\t=(6\pm17.08)/(32)\\t=(6+17.08)/(32) \,\,and\,\, t=(6-17.08)/(32)\\t=0.721\,\,and\,\, t=-0.34`

Since time cannot be negative, so t = 0.721 or 0.72

So, Option A is correct