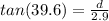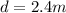Question

A narrow beam of light from a laser travels through air (n = 1.00) and strikes the surface of the water (n = 1.33) in a lake at point A. The angle of incidence is 58 degrees. The depth of the lake is 2.9 m. On the flat lake-bottom is point B, directly below point A. (a) If refraction did not occur, how far away from point B would the laser beam strike the lakebottom? (b) Considering refraction, how far away from point B would the laser beam strike the lake-bottom?

Answer 1

Part a)

d = 4.64 m

Part b)

d = 2.4 m

Step-by-step explanation:

Part a)

If no refraction occurs then the light ray will move undeviating

So here we can say that the angle with the normal will remain same

so we have

`tan\theta = (d)/(h)`

`tan58 = (d)/(2.9)`

`d = 4.64 m`

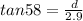
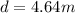
so light will strike at distance of 4.64 m

Part b)

Now if refraction of light occurs

then we will use Snell's law

`n_1sin\theta_1 = n_2 sin\theta_2`

`1.00 sin58 = 1.33sin\theta`

`\theta = 39.6 degree`

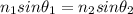
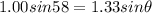
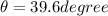
now we can use

`tan\theta = (d)/(h)`

`tan(39.6) = (d)/(2.9)`

`d = 2.4 m`