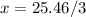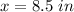Question

HELP PLEASE! Find the height of the triangle by applying formulas for the area of a triangle and your knowledge about triangles.

A. 8 in.
B. 11.3 in.
C. 8.5 in.
D. 6.2 in.

Answer 1

Option C. 8.5 in.

Explanation:

see the attached figure with letters to better understand the problem

we know that

The formula of area of triangle is equal to

`A=(1)/(2)(b)(h)`

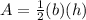
In this problem

we have

`b=BC=6\ in`

`h=AD=x\ in`

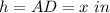
substitute

`A=(1)/(2)(6)(x)`

`A=3x\ in^(2)` ------> equation 1

Remember that

Heron's Formula is a method for calculating the area of a triangle when you know the lengths of all three sides.

Let

a,b,c be the lengths of the sides of a triangle.

The area is given by:

`A=√(p(p-a)(p-b)(p-c))`

where

p is half the perimeter

p=
`(a+b+c)/(2)`

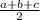
we have

`a=9\ in`

`b=9\ in`

`c=6\ in`

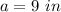
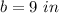
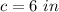
Find the half perimeter p

p=
`(9+9+6)/(2)=12\ in`

Find the area

`A=√(12(12-9)(12-9)(12-6))`

`A=√(12(3)(3)(6))`

`A=√(648)`

`A=25.46\ in^(2)`

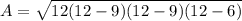
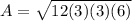
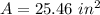
Substitute the value of the area in the equation 1 and solve for x

`A=3x\ in^(2)`

`25.46=3x`

`x=25.46/3`

`x=8.5\ in`