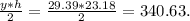Question

In \triangle ABC, we have \angle BAC = 60^\circ and \angle ABC = 45^\circ. The bisector of \angle A intersects \overline{BC} at point T, and AT = 24. What is the area of \triangle ABC?

Answer 1

340.63

Explanation:

To find the area we need to calculate the height of the triangle and one of its sides. the bisector cuts the 60° angle in two of 30°. In the picture I drew the triangle and the sides we need to calculate are y and h.

`\angle C = 180-45-60= 75.`

`\angle ACT = 180-30-75 = 75.`

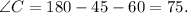
We are going to calculate x, y and h with sin law:

`(x)/(sin(75))= (24)/(sin(75))`

`x= (24*sin(75))/(sin(75))=24.`

`(y)/(sin(60))= (24)/(sin(45))`

`y= (24*sin(60))/(sin(75))=29.39.`

`(h)/(sin(75))= (24)/(sin(90))`

`h= (24*sin(75))/(sin(90))=23.18.`

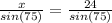
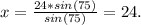
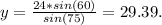
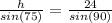
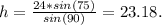
Then, the area of the triangle is

A =
`(y*h)/(2) = (29.39*23.18)/(2)= 340.63.`