Question

Jane was given a bag of sweets and ate two-thirds of them right away. The next day she ate two-thirds of the remainder and the following day she ate two-thirds of the remaining candy before stopping. Only 2 pieces of candy were left. How many sweets was he given in the beginning?

Answer 1

54

Explanation:

First you take two and multiply it by three, which gives you 6. Then you multiply it by three and get 18. Then you multiply and get 54.

Answer 2

54

Explanation:

Let the initial amount of sweets be x

Jane ate two-thirds of them =
`(2)/(3)x`

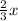
Remaining sweets =
`x-(2)/(3)x`

=
`(1)/(3)x`

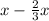
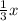
The next day she ate two-thirds of the remainder i.e.
`(2)/(3) * (1)/(3)x =(2)/(9)x`

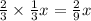
Remaining sweets =
`(1)/(3)x-(2)/(9)x`

=
`(1)/(9)x`

The following day she ate two-thirds of the remaining candy before stopping.

She ate =
`(2)/(3) * (1)/(9)x =(2)/(27)x`

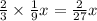
Remaining sweets =
`(1)/(9)x-(2)/(27)x=(1)/(27)x`

Now we are given that Only 2 pieces of candy were left

So,
`(1)/(27)x=2`

`x=2 * 27`

`x=54`

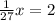
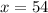
Hence she has given 54 sweets in the beginning.