Question

A particle is moving with the given acceleration function and initial conditions. Find the velocity function and the position function of this particle. a(t) = 2 sin(t) − 4 cos(t), v(0) = −3, s(0) = 5

Answer 1

The velocity function is the particle is
`v(t)=-2\cos (t)-4\sin (t)-1`.

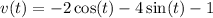Explanation:

The acceleration function of a moving particle is

`a(t)=2\sin (t)-4\cos (t)`

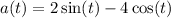
The initial conditions are v(0) = −3, s(0) = 5.

Integrate the acceleration function with respect to time to find the velocity function.

`\int a(t)=\int (2\sin (t)-4\cos (t))dt`

`v(t)=-2\cos (t)-4\sin (t)+C_1`

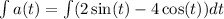
Use the initial condition v(0) = −3 to find the value of C₁.

`-3=-2\cos (0)-4\sin (0)+C_1`

`-3=-2(1)-4(0)+C_1`

`-3=-2+C_1`

`-3+2=C_1`

`-1=C_1`

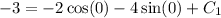
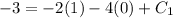
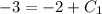
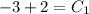
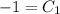
So the velocity function is the particle is

`v(t)=-2\cos (t)-4\sin (t)-1`

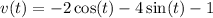
Integrate the acceleration function with respect to time to find the position function.

`\int v(t)=\int (-2\cos (t)-4\sin (t)-1)dt`

`s(t)=-2\sin (t)+4\cos (t)-t+C_2`

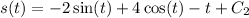
Use the initial condition s(0) = 5 to find the value of C₂.

`5=-2\sin (0)+4\cos (0)-(0)+C_2`

`5=-2(0)+4(1)+C_2`

`5=4+C_2`

`1=C_2`

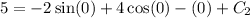
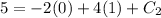
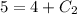
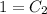
So, the position function is the particle is
`s(t)=-2\sin (t)+4\cos (t)-t+1`.