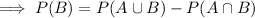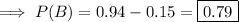We're told that
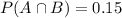
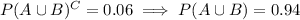
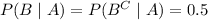
where the last fact is due to the law of total probability:

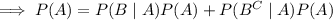
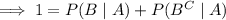
so that
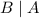 and
and
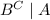 are complementary.
are complementary.
By definition of conditional probability, we have
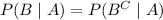
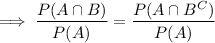
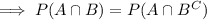
We make use of the addition rule and complementary probabilities to rewrite this as
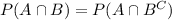
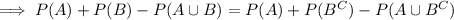
![\implies P(B)-[1-P(A\cup B)^C]=[1-P(B)]-P(A\cup B^C)](https://img.qammunity.org/2020/formulas/mathematics/college/w7yt5b6srev0y8bpnlp708c68nfkhbuu85.png)
![\implies2P(B)=2-[P(A\cup B)^C+P(A\cup B^C)]](https://img.qammunity.org/2020/formulas/mathematics/college/dcmwaopwei1ij22ui6s4vvioswhuc2yplx.png)
![\implies2P(B)=[1-P(A\cup B)^C]+[1-P(A\cup B^C)]](https://img.qammunity.org/2020/formulas/mathematics/college/3fdh0rzq77nycap1qbb2c59qvao1bv9781.png)
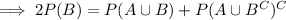

By the law of total probability,
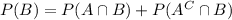
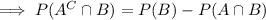
and substituting this into
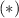 gives
gives
![2P(B)=P(A\cup B)+[P(B)-P(A\cap B)]](https://img.qammunity.org/2020/formulas/mathematics/college/7a1pt7vvxzd3jxkrihp9nntporcketliio.png)