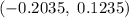Answer:
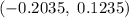
Explanation:
The confidence interval for the difference of two population proportion is given by :-
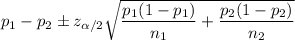
Given :

The proportion of students in the first sample replied that they turned to their mother rather than their father for help. =
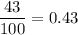
The proportion of students in the second sample replied that they turned to their mother rather than their father for help. =
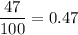
Significance level :

Critical value :
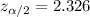
Now, the 98% confidence interval for
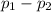 will be :-
will be :-
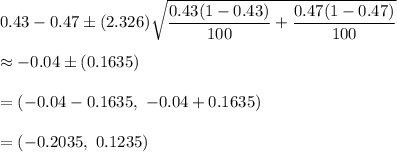
Hence, the 98% confidence interval for
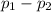 is
is