Answer:
It will be a better offer the option B because it yield a higher net present value at the given rate.
B 88,457
A 86,755
C 85,000
Step-by-step explanation:
We are going to compare the present value of each annuity at the cost of capital rate 7.5%

option A
C= couta, monthly payment 1,500
rate= 0.075 is an annual rate we divide by 12 to get the monthly rate
time = 6 years = 6*12 = 72 months
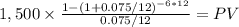
option A PV = 86,754.78646
option B
C = 1,050
time = 10 years
same rate
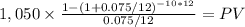
option B PV = 88,456.97984
option C = 85,000
It will be a better offer the option B because it yield a higher net present value at the given rate.