Question

The length of time it takes college students to find a parking spot in the library parking lot follows a normal distribution with a mean of 55 minutes and a standard deviation of 1 minute. Find the probability that a randomly selected college student will take between 3.53.5 and 66 minutes to find a parking spot in the library lot.

Answer 1

Answer: 0.7745

Explanation:

Given : The length of time it takes college students to find a parking spot in the library parking lot follows a normal distribution with

`\mu=5\text{ minutes}`

Standard deviation :
`\sigma=1\text{ minute}`

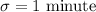
Let x be the random variable that represents the length of time it takes college students to find a parking spot .

Z-score :
`z=(x-\mu)/(\sigma)`

For x = 3.5 minutes

`z=(3.5-5)/(1)=-1.5`

For x = 6 minutes

`z=(6-5)/(1)=1`

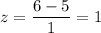
Now, the probability that a randomly selected college student will take between 3.5 and 6 minutes to find a parking spot in the library lot will be :-

`P(3.5<X<6)=P(-1.5<z<1)\\\\=P(z<1)-P(z<-1.5)\\\\= 0.8413447-0.0668072=0.7745375\approx0.7745`

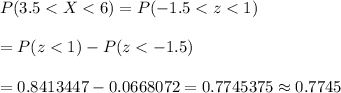
Hence, the probability that a randomly selected college student will take between 3.5 and 6 minutes to find a parking spot in the library lot will be 0.7745.