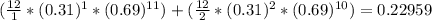Answer:
a) 0.23235
b) 0.53806
c) 0.22959
Explanation:
Given-
Adults having cashews as their favorite kind of nut
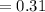
Adults not having cashews as their favorite kind of nut
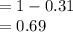
a) Exactly three
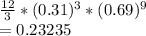
Thus, the probability that three adults have cashews as are their favorite nut is 0.23235
b) at least four
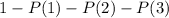
![1-[({(12)/(1) * (0.31)^1* (0.69)^(11))+({(12)/(2) * (0.31)^2* (0.69)^(10))+({(12)/(3) * (0.31)^3* (0.69)^(9))]](https://img.qammunity.org/2020/formulas/mathematics/high-school/sx8loxfyu8xsgdmflkgmpov0j87t7a7ync.png)
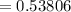
c) at most two