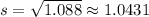Question

Sixty-eight percent of adults in a certain country believe that life on other planets is plausible. You randomly select five adults and ask them whether they believe that life on other planets is plausible. The random variable represents the number of adults who believe that life on other planets is plausible. Find the mean, variance, and standard deviation of the binomial distribution for the random variable. Interpret the results.

Answer 1

Mean = 3.4

Variance = 1.088

Standard deviation = 1.0431

Explanation:

`P=0.68\\ \\N=5`

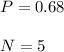
The mean of a binomial distribution with parameters N (the number of trials) and p (the probability of success for each trial) is
`m=N\cdot p`

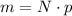
Thus,

`m=5\cdot 0.68=3.4`

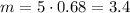
The variance of the binomial distribution is
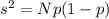`s^2=Np(1-p)`, where
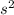`s^2`​​ is the variance of the binomial distribution, so

`s^2=5\cdot 0.68\cdot (1-0.68)=3.4\cdot 0.32=1.088`

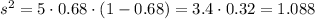
The standard deviation
`s` is the square root of the variance
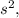`s^2,` so

`s=√(1.088)\approx 1.0431`