Question

A voltage V is applied to the primary coil of a step-up transformer with a 3:1 ratio of turns between its primary and secondary coils. A resistor R connected to the secondary dissipates a power P = 100 W. How much power is dissipated by the same resistor when the ratio of turns in the transformer is changed to 24:1 and the same input voltage is used?

Answer 1

Step-by-step explanation:

Let
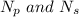`N_p\ and\ N_s` are the number of turns in primary and secondary coil of the transformer such that,

`(N_p)/(N_s)=(1)/(3)`

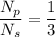
A resistor R connected to the secondary dissipates a power
`P_s=100\ W`

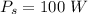
For a transformer,
`(N_s)/(N_p)=(V_s)/(V_p)`

`V_s=((N_s)/(N_p))V_p`

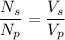
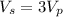`V_s=3V_p`...............(1)

The power dissipated through the secondary coil is :

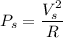
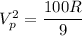`P_s=(V_s^2)/(R)`

`100\ W=(V_s^2)/(R)`

`V_p^2=(100R)/(9)`.............(2)

Let
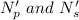`N_p'\ and\ N_s'` are the new number of turns in primary and secondary coil of the transformer such that,

`(N_p')/(N_s')=(1)/(24)`

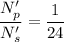
New voltage is :

`V_s'=((N_s')/(N_p'))V_p'`

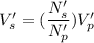
`V_s'=24V_p`...............(3)

So, new power dissipated is
`P_s'`

`P_s'=(V_s'^2)/(R)`

`P_s'=((24V_p)^2)/(R)`

`P_s'=24^2* ((V_p)^2)/(R)`

`P_s'=24^2* (((100R)/(9)))/(R)`

`P_s'=6400\ Watts`

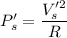
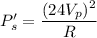
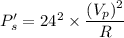
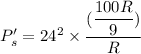
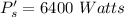
So, the new power dissipated by the same resistor is 6400 watts. Hence, this is the required solution.